Game Theory

Game theory is the mathematical study of the conflicts and strategies analyzed to make the most efficient decision, based on preordained rules. Written game theory analogies can be organized into quadrants representing each possible outcome based on a different course of action. Game theory serves as a valuable structure for conceptualizing the decision making process.

The Prisoner’s Dilemma

The prisoner’s dilemma shows how two individuals may not cooperate although it is in their best interest to do so. Under this game theory analogy, two prisoners have been apprehended and await trial. They each have two options: betray the other or remain silent. If both prisoners betray one another, they will both receive a two year sentence. If both prisoners remain silent, they will both serve a one year sentence. If one prisoner betrays and the other is silent, the silent prisoner receives the full punishment, which carries a three-year prison sentence. Accordingly, a rational prisoner will betray his counterpart in an act of self-preservation, even though the optimal mutually beneficial solution would be to cooperate.

The Byzantine Generals Problem

The Byzantine Generals Problem is a well-known game theory analogy. The analogy begins with several generals attacking Byzantium. They have surrounded the city, and they must collectively decide when to attack. The generals cannot securely communicate because any messages they send or receive may have been intercepted or deceptively sent by Byzantium’s centralized defenders. If all generals attack simultaneously, they will win, but they will lose if they strike at different times.

Decentralized systems face the Byzantine Generals Problem because there is no centralized entity verifying information for members of the network. Centralized systems do not face this problem because network members accept the risk of trusting an intermediary, thus defeating the purpose of this game analogy. If the generals could trust an intermediary, this game theory analogy would not exist in the first place.

– Satoshi Nakamoto explaining the predominant flaw with fiat money.

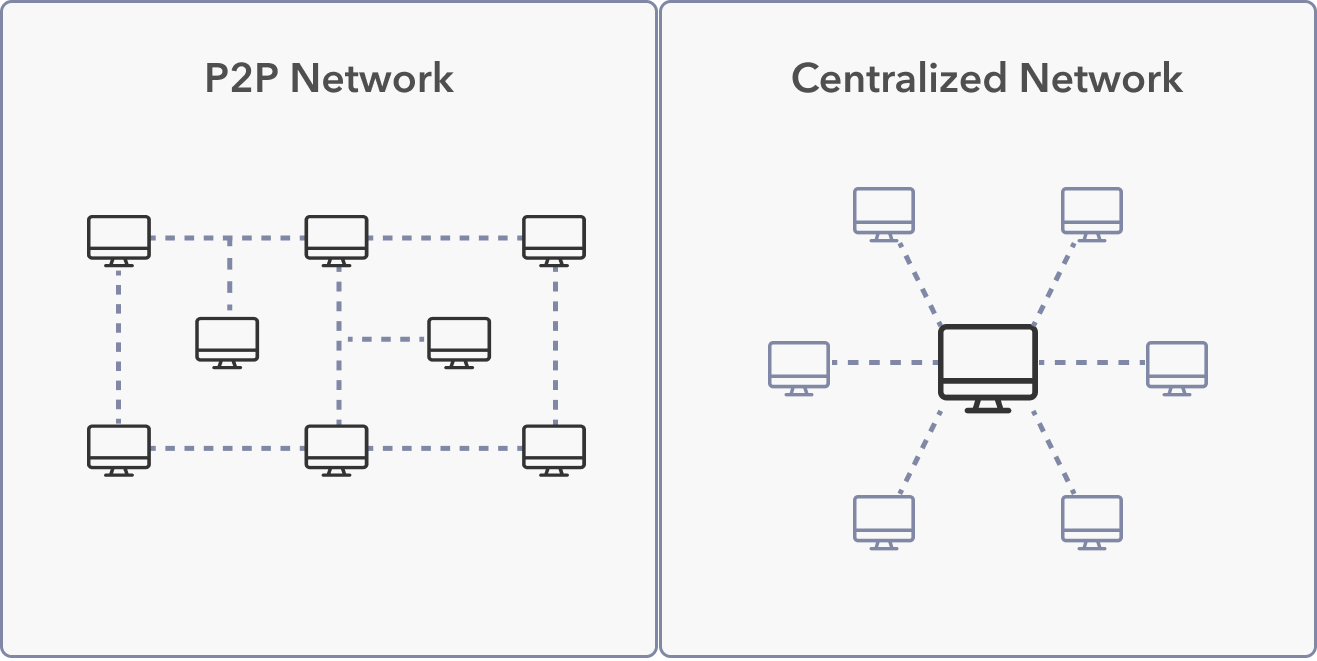
The Byzantine Generals Problem has become increasingly popular because Bitcoin’s Proof-of-Work algorithm was the first theoretically sound solution to this problem. Decentralized money faces and must overcome the Byzantine Generals Problem, as it requires members of a decentralized and widespread group to reach consensus on the value of a medium of exchange.

➤ Learn more about game theory behind the Byzantine Generals Problem.

Nash Equilibrium

Sometimes participants in a game theory analogy reach a stalemate, called a Nash equilibrium. At a Nash equilibrium, no individual player can benefit from a unilateral change in strategy. At this point, the player can only improve the expected payoff with the help of another player.

Analyzing Nash equilibriums in different game theory situations can provide insight into how some decisions are suitable for an individual player but have proportionally worse consequences for the rest of the parties involved in the game.